Let’s talk (or write, actually) about our favorite node. Grade might be (or at least one of) the most used node in Nuke, and a lot of believes make it a not so well understood node. As always, in case of doubt, just look at the source. And again, the Foundry is kind enough to give us the source code for our beloved Grade. So lets dig into it and see what we can learn.
The first (and main) common error concerns the operation order of the node. I’ve seen and heard a few (wrong) assumptions on how these knobs interact with each other. It turns out, one of the first lines of the source code gives us the help information for the node, containing Grade’s equation ! So now is time for the truth to be told.
A = multiply * (gain-lift)/(whitepoint-blackpoint)
B = offset + lift - A*blackpoint
output = pow(A*input + B, 1/gamma)Gain ≠ multiply
I always heard and said that gain and multiply are the same; whilst not being entirely false (it does a multiplication), both nodes don’t operate in the same place in the equation, giving different results in some cases. I experienced this when doing the good old trick of fog with Zdepth. We all know it, remapping the depth, shuffling it in alpha and, amongst a lot of possibilities, plugging it in a grade’s mask and lift. The problem is it will brighten the whole masked area, and will give this brighten look instead of foggy look. Of course we can use other operations more suited to avoid brightening the picture; but one trick is to multiply down while lifting. This will squeeze the contrast of the area and give a dense fog sensation.
As you saw, I wrote multiply down, and not gain down. This is, at least for me, where both knobs act differently. If you gain down to 0 and lift up, you’ll see your picture break, while multiply won’t bring your values below lift’s value. The equation helps understand this behavior. As lift subtracts gain, if gain < lift, then A is negative, it will multiply your input thus making it negative. Then B is added, which is equivalent to lift if blackpoint = 0 (default value). So if your pixel is bright:
pixel = 1.0
lift = 0.1
gain = 0
multiply = 1 //Default value
A = multiply * (gain-lift)/(whitepoint-blackpoint)
A = 1*(0-0.1)/1
A = - 0.1
B = lift = 0.1
out = A*pixel + B //Ignore gamma for now
out = - 0.1 * 1 + 0.1
out = 0Hence your bright pixel becomes totally black, while your dark pixels are lifted, creating a negative-like picture. If multiply=0, A=0 so basically return input*0+B, thus not inverting your dynamic.
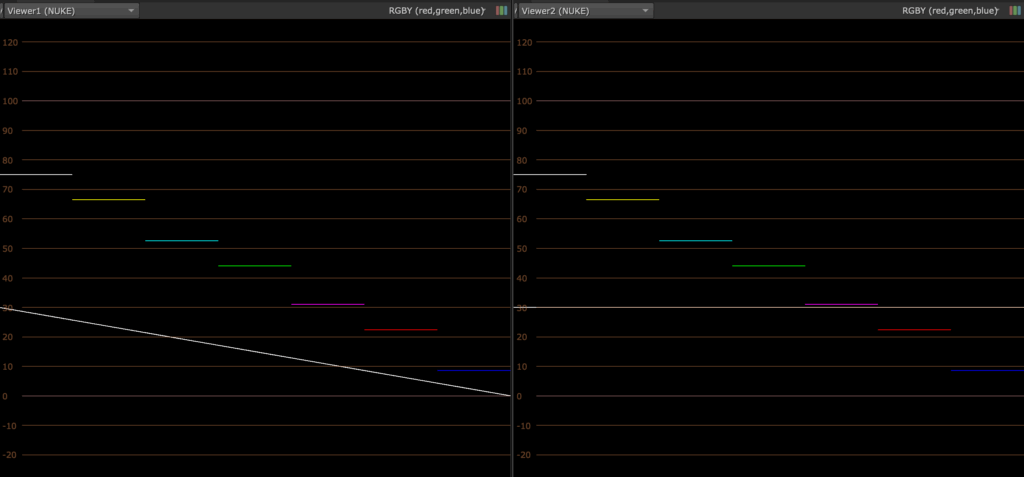
You’ll want to set your viewerProcess to None to avoid viewer transform to affect the shape of the curve. Or you can disable the viewer process in the scope by going to Preferences -> Scopes and uncheck Include viewer color transforms.
Gamma is not an actual gamma (nor an inverse)
As you surely already know, our gamma know is not an actual gamma, but rather an inverted gamma. This is actually the case for most (if not all ?) grading tools. The reason is quite simple, the gamma value is counter intuitive. We usually separate our dynamic into three groups : shadows, midtones, highlights; and every group as its dedicated knob : shadows-lift, midtones-gamma, highlights-gain/multiply. For each knob, a higher value means a brighter output, except for (real) gamma.
Gamma is a power operation, which putting a gamma of 2 on pixel value 0.5 gives 0.52. As you can see 0.52 doesn’t give a higher value than 0.5, it actually gives 0.25. So for value between 0 and 1 (excluded), a higher gamma gives a lower output. So to avoid confusion, the gamma value is usually inverted before being applied to our input, hence our equation (A*input + B)1/gamma.
Yes, I know you knew that, but..
There’s another catch, which isn’t to be found in the equation. Actually, the above equation is false and doesn’t represent the actual « gamma » operation inside our Grade, which is neither a gamma nor an inverse gamma. Let’s go lower in the code.
// do the gamma:
if (G <= 0) {
std::transform(inBegin, inBegin+w, outptr,
[](const float x) {
if (x < 0.0f)
return 0.0f;
if (x > 1.0f)
return INFINITY;
return x;
}
);
}
else if (G != 1.0f) {
G = 1.0f / G;
std::transform(inBegin, inBegin+w, outptr,
[G](const float x) {
if (x < 0.0f)
return x;
if (x < 1.0f)
return powf(x, G);
return 1.0f + (x - 1.0f) * G;
}
);
}
else if (inBegin != outptr) {
std::copy(inBegin, inBegin+w, outptr);
}What’s interesting to us is in the else if (G != 1.0f) statement. We can see that if our channel value < 1, it does an actual power function like we’d expect. However, if our channel value is above 1, it does this strange operation : 1.0f + (x – 1.0f) * G (x being our channel value, and G our inverted gamma value).
What does it do ? Well, the way a power function works is by multiplying a value by itself a certain amount of time, which can lead your output value to brighten up very rapidly; so if you gamma down, your highlight can quickly go in the range of thousands if not more, which can be a problem. So to avoid this behavior, if our input value is above 1, our Grade won’t do a power function on in, but will rather apply a linear function. A way of seeing this operation is through the derivative. It basically takes the derivative function of our power function at x = 1, and applies it on all values > 1. What you’ll get is a nice curved power function which becomes linear above 1.
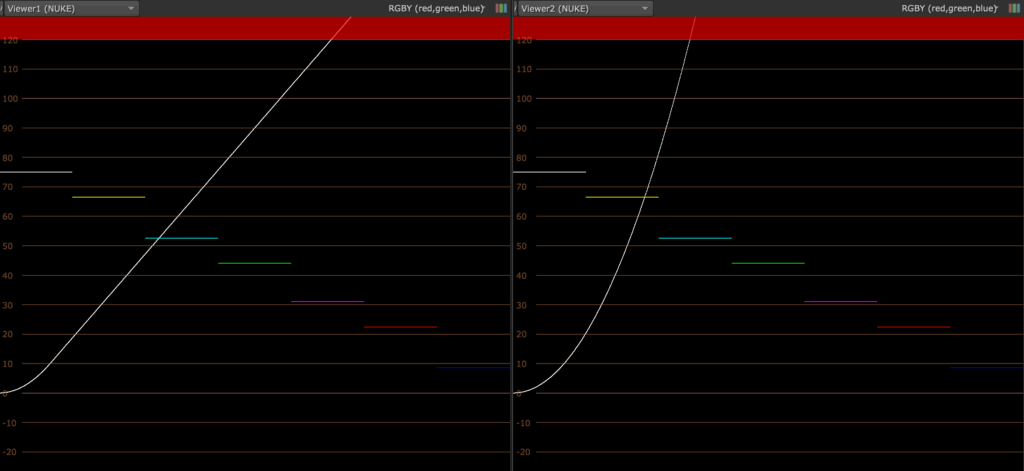
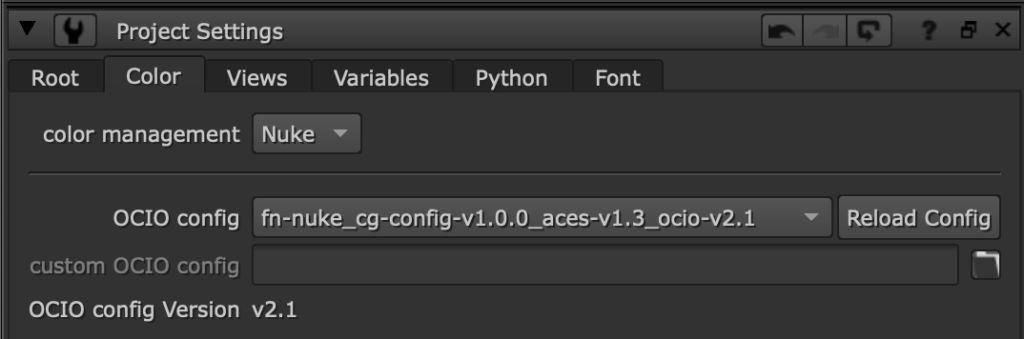
Is it possible to have a real power function in Nuke ? Yes ! The Gamma node applies a real gamma function, as well as the OCIOCDLTransform. If you really need a power function, I’d recommend that you use the Gamma node rather than the OCIOCDLTransform, as this one can have some unwanted effects on values below 0. In fact, as you can see in the above source code, the Grade (and Gamma) node will let negative values untouched (as a real power function would do some funky results); the OCIOCDLTransform, on the other hand, will have a different behavior depending on the OCIO version you’re using. With OCIO v2, it will do the same as the other nuke’s node, but with OCIO v1, negative values will be clamped to 0; (I honestly don’t see a case where this would be desirable). In case you doubt on which OCIO version you’re using, you can check in your project settings into the Color tab.
Another thing that can be said about gamma, is that power functions are quite computationally expensive and have to be avoided when possible (especially if you’re gonna apply it to 3 channels * 8.8 millions pixels (for a 4k picture). That’s why Grade node’s has a method isGammaConstantOne which checks if gamma knob is set to 1, and isn’t animated. This is good to know as if your gamma is set to 1 (hence unchanged) but your knob is set animated, Nuke will still compute this expensive function, this won’t do much on a single node, but this should still be avoided as, as this kind a small mistake multiplies, it can really slow down your comp. This method’s comment is here to tell us the good behavior :
/// (Note: There is the possibility that gamma is set as animated but in fact all the keys have
/// a value of 1, in which case we’d needlessly pay the cost of the pow() calls, but that’s
/// unlikely and something we should encourage users to avoid.)
Grade does NOT concatenate
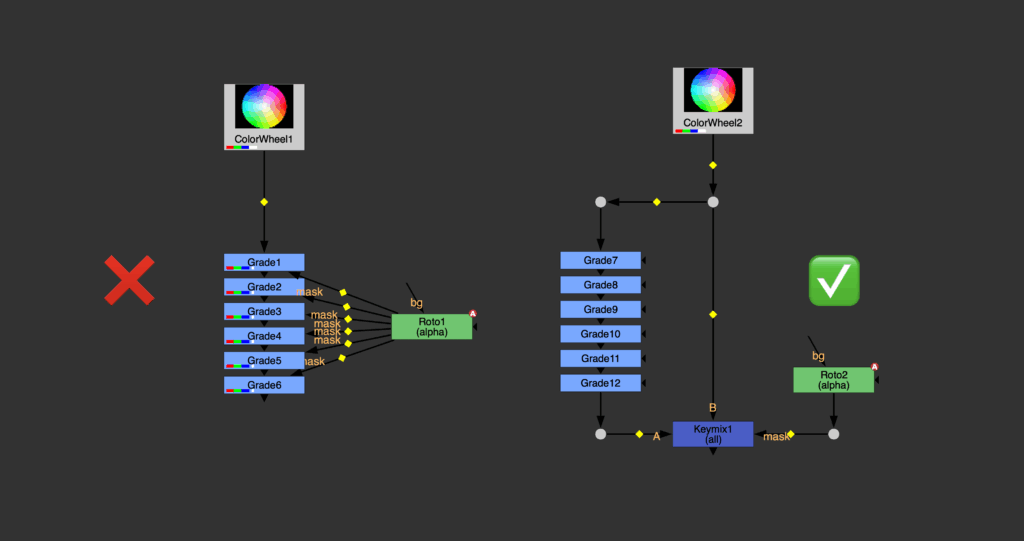
I can’t remember how many times I’ve had this debate, and I don’t know where this belief comes from. But no. Grades don’t concatenate in your comp. I don’t think Foundry ever said anything or insinuated that they do. But it is said clearly in Nuke’s documentation about concatenation that « Color nodes do not concatenate because Nuke works in a 32-bit float, which is enough to avoid banding and visible round-off errors in color. » A good clue, in my opinion, to detect that a node can’t concatenate, is the presence of the mask input. That fact that a mask can constrain an effect breaks any « uniformity », the transformation isn’t the same over the whole picture and can’t really be transferred to the next node. That’s why Transform node do concatenate, but TransformMasked don’t.
Also plugging a mask really breaks the linearity of an effect, that’s why you shouldn’t plug a mask to multiple nodes in a row; instead, stack all your nodes on a side, then merge them with a Keymix which will apply the mask only once.
Power fucks things up
I got stuck with this concatenation problem for quite a while, and I wondered if Grades could actually concatenate, supposing that we don’t mask and just.. grade.
The simple answer is, no. The complex answer is, it actually depends on what your grade is doing. As we saw earlier, Grade’s equation is mostly linear; and it is totally possible to combine multiple linear curve. So you could combine multiple Grades into one, until you start playing with the gamma knob. At this point, the curve isn’t linear anymore and combining them into a single grade-like curve (affine + gamma) is unlikely.
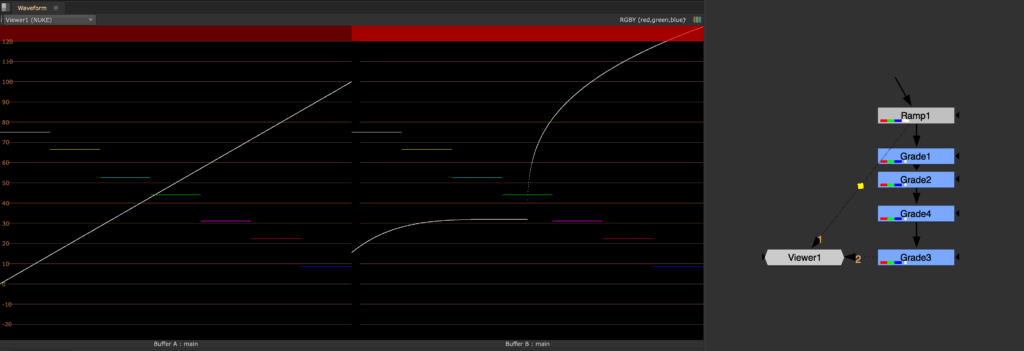
All these make quite complicated to concatenate Grades, a lot of conditions have to be reunited to make it possible, and this makes it easier to rely on the pretty large space that 32 bit float gives us, so that we can play freely with multiple nodes without risking (too much) to break our pixels.
Here’s for some common Grade misconceptions, I guess there’s more to discover and explore. Until then, I hope you’ve enjoyed reading this article, and gained from it; or multiplied.. can’t remember which is which.